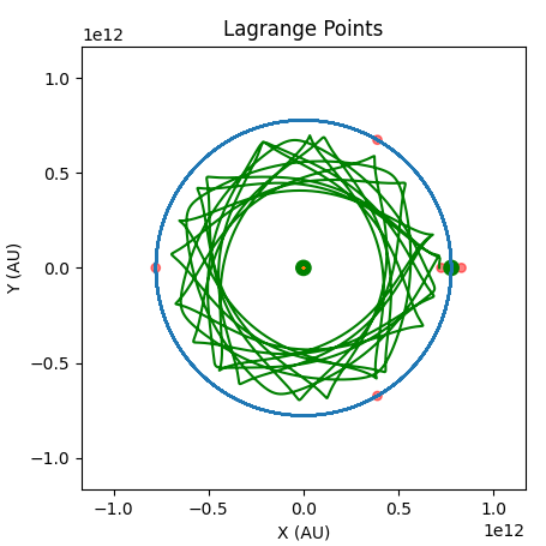
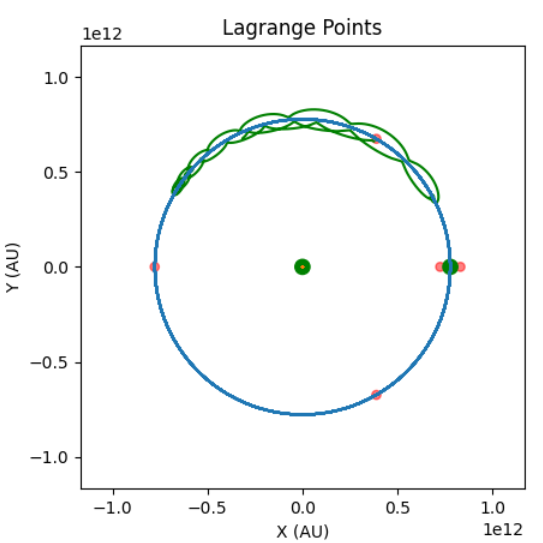
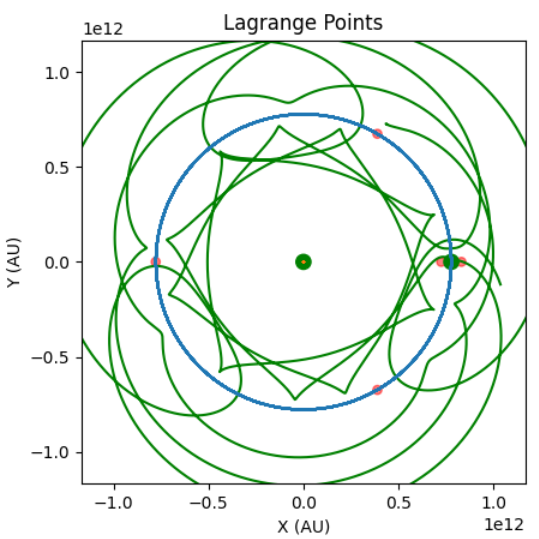
Lagrange points are areas in space formed in any 2 body system. When a mass is at a lagrange point, it will not move relative to those two bodies. This simulation fixes the reference frame so that the two bodies appear stationary, and the test mass orbits relative to them. For this simulation, the masses of the Sun and Jupiter were used. The python scripts used to generate all of the images on this page can be found in our GitHub repository.
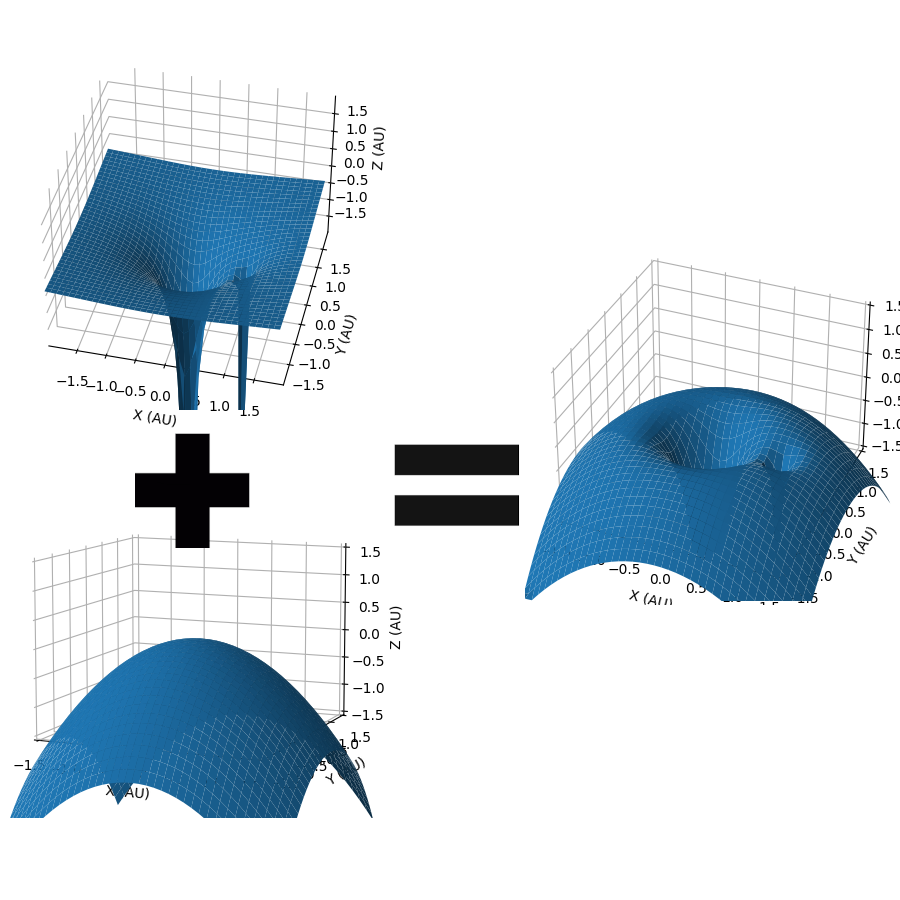
The L points can be grouped into 2 categories, stable and unstable. L4 and L5 are stable, whereas points 1 through 3 are unstable. This is because of their effective potential:
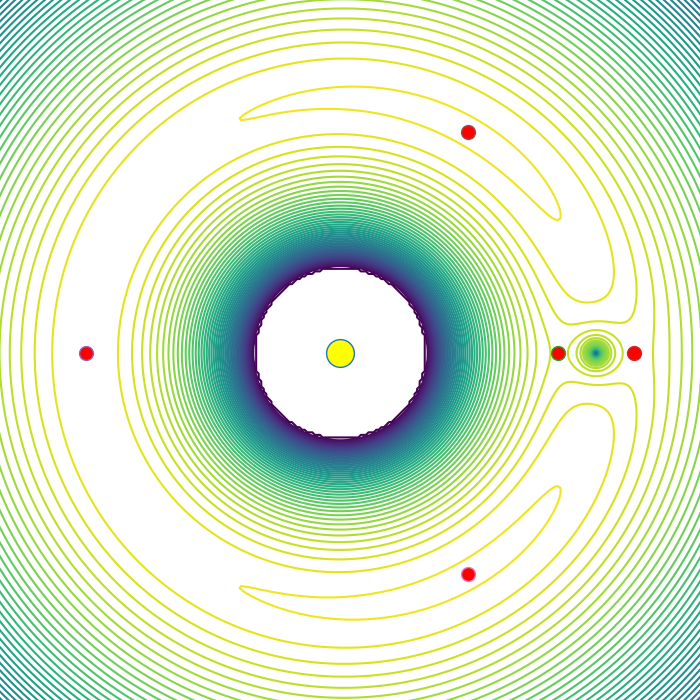
As you can see, L4 and L5 form peaks, whereas L1, L2 and L3 form saddles. This may seem counterintuitive, as usually peaks of potential are unstable. However, as we are in a rotating reference frame, the coriolis force takes effect. This sends the mass into an orbit around the point, making them considered stable. So stable in fact, that asteroids often find themselves trapped within an L point. Jupiter has many such asteroids, called "trojan asteroids". The other lagrange points however need adjustment every 20 or so days in order to stay within them. However these points still reduce fuel consumption, and we have many monitoring stations and telescopes placed at points L1 and L2.