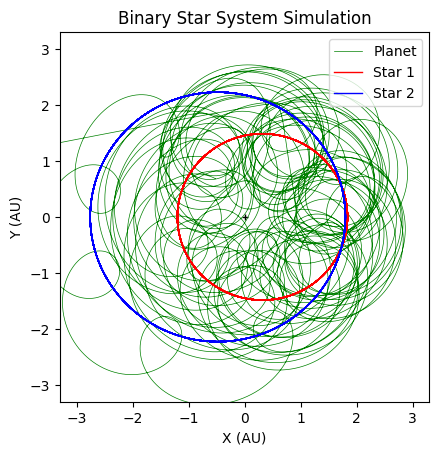
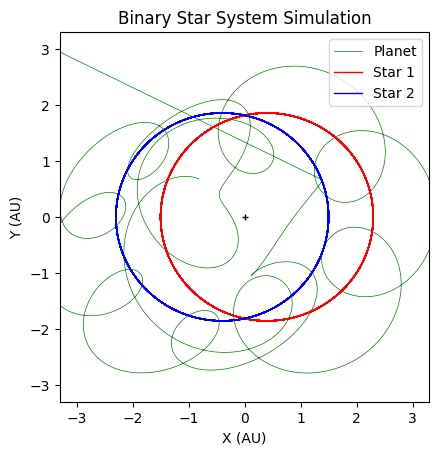
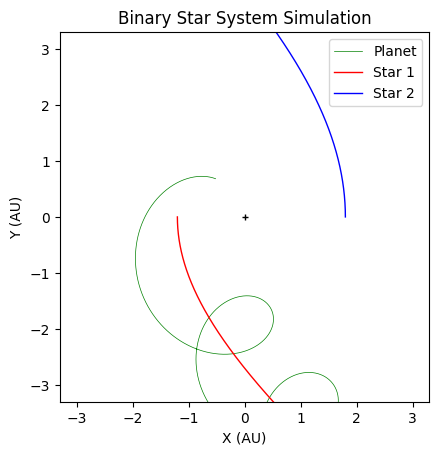
The Binary systems model shows a system such that there are 2 stars of arbitrary mass( measured in solar masses)
and 1 planet where the mass is treated as negligible.
The planets have an inital seperation equal to their semi-major axis(a) and the distance from the center of mass
of the 2 stars to each star is determined from the following equations:
$$r_{1} = a\frac{M1}{M1 + M2}$$
$$r_2 = a - r_1$$
Time increments in small steps, where at each step acceleration for both stars and the planet is calculated
using newtons law of gravitation:
$$a_{n,i} = -G\sum_{j\ne i}^{N}M_j\frac{r_i-r_j}{\left|r_i-r_j \right|^3}$$
The new position of each planet is then calculated using the verlet method shown below:
$$a_n = f(t_n, r_n, v_n)$$
$$t_{n+1} = t_n +\Delta t$$
$$r_{n+1} = r_n + v_n\Delta t + \frac{1}{2}a_n\Delta t^2$$
$$V = v_n + a_n\Delta t$$
$$A = f(t_{n+1}, r_{n+1}, V)$$
$$v_{n+1} = v_n + \frac{1}{2}(a_n +A)\Delta t$$
The time then continues incrementing until a set number of orbits has been achieved. The orbital paths are then
plotted and outputted as a graph.
The model can also be animated and an example video accompanies this page to demonstrate the animated model.
Note: Due to issues with Python animation website integration, a .mp4 file of an example animation is presented
to the user, whom we invite to download the python file if they wish (all Python files can be found within the
Task files folder of the Github Repository).