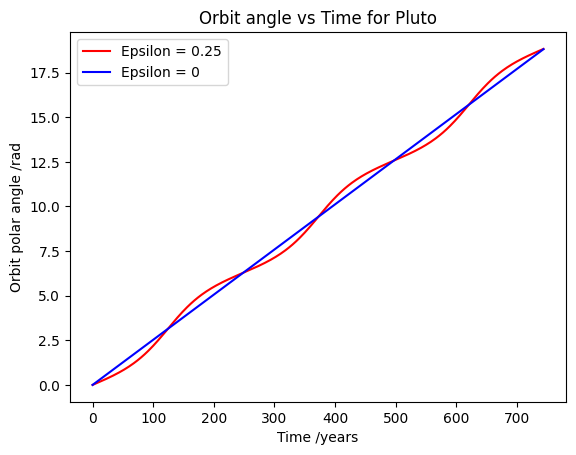
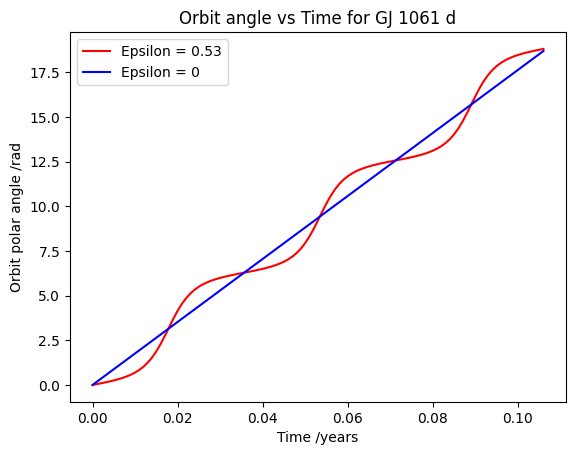
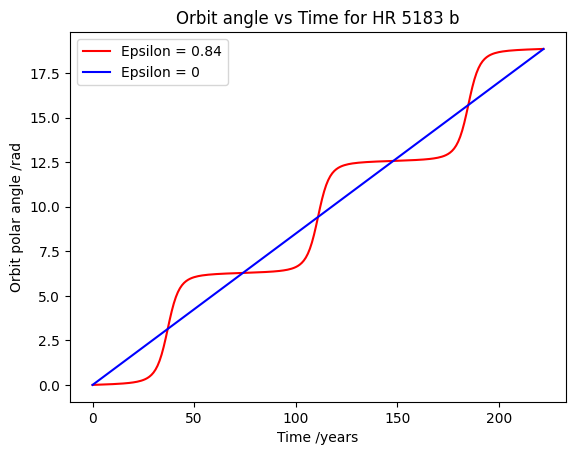
Task 5 outputs a graph for the polar angle based on the orbital time for the planet.
A graph is generated by incrementing time in small amounts to plot the orbital angle for the planet for when its eccentricity is 0 (a circular orbit) or its actual value.
This is done by interpolating the following function:
$$t = P(1-\varepsilon^2 )^\frac{3}{2}\frac{1}{2\pi }\int_{{\theta}_0 }^{\theta}\frac{d\theta}{(1-\varepsilon cos\theta)^2}$$
This function is evaluated using Simpson's numeric method:
where $$h = \frac{b-a}{N}$$
In order to improve the efficency of the code the time increment is pre-determined and varies per planet to compensate for longer or shorter orbital periods.
The number of subintervals (N) for Simpson's numeric method is 1000 to ensure accuracy.